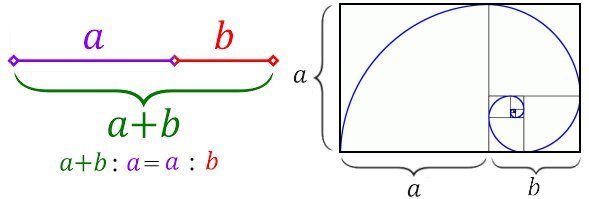
Una persona gentile mi ha chiesto di parlare di ϕ (o phi, da leggere “fi”), il numero aureo o sezione aurea. Accetto, anche se in proposito si trovano siti, video e libri ben fatti ed esaurienti. Phi è il numero (1+√5)/2. E’ irrazionale e algebrico (ho spiegato qui questi termini). La sua fama è dovuta a una proporzione, chiamata divina da Luca Pacioli, ritenuta gradevole alla vista: il rapporto fra due segmenti “a” e “b” che sia uguale al rapporto fra la loro somma e il più lungo dei due, cioè “(a+b):a = a:b”. Da una nota regola (il prodotto degli estremi è uguale al prodotto dei medi) si ricava un’equazione di secondo grado, la cui soluzione positiva è appunto a/b = ϕ. Un rettangolo con lati di lunghezze a+b ed a, dove a/b = ϕ, risulta particolarmente armonioso, forse per una bella proprietà geometrica: se dal rettangolo si toglie un quadrato di lato a, il rettangolo rimanente ha i lati nello stesso rapporto. Un fantastico film del 1959, Paperino nel mondo della Matemagica, ci ricorda che questo rettangolo compare ripetutamente nel Partenone e nella costruzione di una bella spirale, presente anche nei girasoli, in certe conchiglie e negli alveari.
La sezione aurea fu studiata dalle scuole di Pitagora e di Euclide ma pare fosse conosciuta anche da Babilonesi ed Egizi; infatti in certe steli e nella piramide di Cheope ci sono lati che approssimano il famoso rapporto. Ma ben più tardi, nella Grande Moschea di Kairouan e nell’opera di Le Corbusier, troviamo un uso frequente di ϕ. Questo numero non ha affascinato solo gli architetti: Leonardo nell’Uomo Vitruviano e Dalì nell’Ultima Cena usano ϕ in modo consapevole; ma – che sia per calcolo o per puro senso estetico – ϕ si ritrova nelle sculture di Fidia e in diversi dipinti dello stesso Leonardo, compresa la Gioconda. Ha poi ispirato esplicitamente molti pittori più recenti, a partire da Sérusier e passando per il cubismo. Ma perfino nella musica ci sono stati, da parte di Bartók e Débussy (ma anche dei Genesis), esperimenti di uso di ϕ.
Dal punto di vista matematico ϕ aveva affascinato i Greci, perché è il rapporto fra lato e diagonale di un pentagono regolare. Dato il significato esoterico attribuito al pentagramma – un pentagono con le sue diagonali – ciò diede origine a una serie di considerazioni di carattere filosofico-astrologico-mistico in cui non oso avventurarmi. Ci sono poi delle stranezze algebriche: si dimostra che ϕ²=ϕ+1 e che 1/ϕ = ϕ-1, perciò questi tre numeri hanno la stessa coda di decimali. Ma un fatto matematico davvero incredibile è la relazione di ϕ con una celebre successione.
Leonardo Pisano, detto Fibonacci, era il matematico del XIII secolo che introdusse in Europa la notazione posizionale, cioè quella attuale dei numeri. Questa sostituiva i numeri romani e cambiò la vita dei commercianti e degli algebristi. La sua celebrità, però, è legata a un esperimento mentale: supponiamo che ogni coppia di conigli – di più di un mese di età – generi un’altra coppia ogni mese. Quante coppie avrò di mese in mese? Se comincio con una coppia appena nata, dopo un mese ne avrò due; dopo un altro mese avrò le due di prima, una fertile e una no, più una nuova coppia generata dalla coppia fertile, quindi tre; un mese dopo si aggiungono due coppie nate dalle due coppie fertili, quindi ne abbiamo cinque, di cui tre partoriranno il mese dopo; e così via.
Si forma la successione di Fibonacci 1, 1, 2, 3, 5, 8, … in cui ogni numero è la somma dei due precedenti. Questa successione si trova in un insieme stupefacente di ambiti: nei numeri di spirali dei girasoli o delle pigne, nei Fibonacci heap del microprocessore Pentium, nella disposizione di foglie sui rami e addirittura nella teoria delle stringhe in fisica teorica. Bene: man mano che si va avanti nella successione, il rapporto fra due numeri consecutivi si avvicina sempre di più a ϕ!
Riservo poche righe per un cugino umile: √2. È il primo numero irrazionale mai scoperto; ragione di scandalo nella scuola pitagorica – ma forse benefica crisi di crescita, secondo Simone Weil – rivela che lato e diagonale di un quadrato sono incommensurabili (aggettivo spesso usato impropriamente): non esiste unità di misura per cui la lunghezza di entrambi possa essere espressa da numeri interi.

Anche √2 è legato a una bella proporzione, quella adottata dalle norme Uni per i lati dei fogli di carta. Infatti se taglio in due un foglio A3 ottengo due fogli A4 i cui lati sono proporzionali a quelli dell’A3 e a quelli dell’A5 eccetera. Il rapporto fra i lati è √2.
Articolo Precedente
Milano, la circolare della preside scatena la protesta dei genitori: “Sul registro entrate e uscite per il bagno”

Articolo Successivo
L’Aquila 2009-2019 – La scuola è ancora in moduli provvisori: ‘Nei container di lusso lavoriamo per mantenere la comunità’






