Matematica, spesso l’astratto equivale al concreto

La mia maestra, buonanima, c’insegnava con passione la grammatica italiana; la ricordo in imbarazzo solo quando dovette spiegarci cosa rappresentasse un sostantivo astratto: “qualcosa che non si può vedere o toccare; qualcosa che non è davvero reale, ma esiste solo nel pensiero” al che le chiesi: “anche l’anima?”. Non ricordo come si sia tirata fuori da quel mio primo spunto agnostico, in un periodo in cui sulla realtà di certe cose non si discuteva, almeno a scuola.

In fondo quella brava donna non era lontana da ciò che leggo sul Sabatini Coletti: “Astratto: che non deriva dall’esperienza sensibile ma dal puro ragionamento. Privo di legami o riscontri con la realtà.” Questo, però, non corrisponde allo stesso concetto in matematica.

Molti decenni dopo tocca a me essere messo in imbarazzo dall’astrazione. Quando enuncio qualcosa come “Dati n vettori linearmente indipendenti…” gli studenti meno remissivi si chiedono cosa siano questi vettori. Sono i vettori geometrici, cioè i soliti segmenti con un estremo in comune? Se sì, allora che senso ha quel numero n? Non può essere al massimo 3? E se sono segmenti, perché non dico “Dati n segmenti”? (E siano benedetti i pragmatici periti, che queste domande me le sbattono in faccia…) La loro impressione è che io stia parlando del nulla; oppure, ad essere generosi, che io stia parlando di cose comuni, ma oscurandole con un linguaggio fighetto.

A mia discolpa dico subito che alla definizione di spazio vettoriale faccio seguire più di mezz’ora di esempi i più disparati possibile e che spesso arricchisco gli enunciati con riferimenti a quegli stessi esempi. Il problema però rimane e non è facilmente eludibile. Infatti se scegliessi di parlare, in termini più concreti, di segmenti (o di forze, di terne di numeri, o di altri casi particolari) spoglierei la teoria di una delle sue più potenti prerogative: la generalità. (N.B.: molti colleghi compiono questa rispettabilissima scelta, a vantaggio di una maggiore comprensibilità e di un programma più vasto.)

Il passaggio concettuale necessario non è diverso da quello che abbiamo compiuto da piccolissimi: se all’inizio capivamo che mettendo insieme due matite con tre matite ottenevamo cinque matite, ad un certo momento ci siamo liberati del caso particolare e abbiamo tranquillamente cominciato a pensare 2+3=5. Se un bimbo ci chiede “Ma due cosa? Tre cosa?” ci fa sorridere. Riconosciamo che è comodo ragionare con numeri astratti; quell’uguaglianza potrà poi essere applicata a infiniti casi particolari fra cui, certo, le matite. È un’uguaglianza astratta che diventa molte volte concreta.

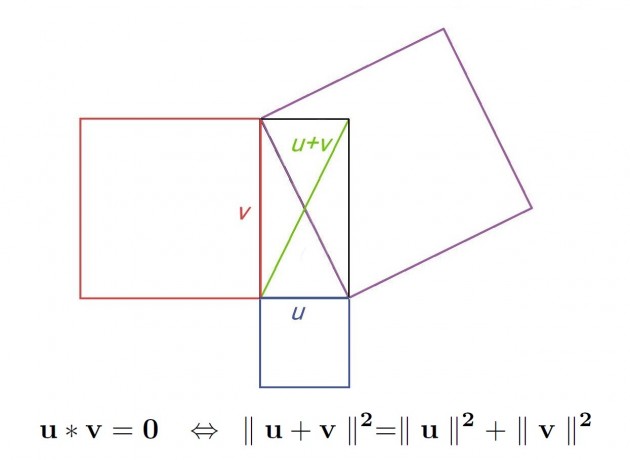
È più difficile, ma più potente, compiere lo stesso salto con la matematica universitaria. L’astrazione, in quanto molteplice concretezza, è ciò che permette delle ricadute impensabili. Prendiamo il caso del teorema di Pitagora. Ne esistono moltissime dimostrazioni di carattere geometrico. Ma fra di loro ce n’è almeno una che riconduce il problema (tramite uno scambio di diagonali, si veda la figura) a una questione vettoriale. L’enunciato prende allora la forma che ho trascritto sotto la figura. Che vantaggio ne traiamo? Solo di avere un modo elegante e moderno (e un bel po’ più criptico…) di dire le stesse cose? No! Immediatamente il teorema ci fornisce una relazione inaspettata fra funzioni, fra matrici, fra tutti gli enti che si possano riconoscere in uno spazio vettoriale e su cui ci sia un prodotto scalare (nel suo senso generalizzato: una volta sarà l’integrale di un prodotto, un’altra sarà la traccia di un prodotto matriciale, ecc.); non ci sono più segmenti, non ci sono angoli né quadrati, ma la relazione sussiste e ci fornisce una conoscenza utile e imprevista!

Lo so, non è facile rinunciare alla semantica in favore della sintassi: dimenticare la sostanza focalizzando l’attenzione solo sulla forma, ignorare la natura delle cose osservandone solo il comportamento. Però è l’unico modo conosciuto per esportare conoscenza in ambiti anche lontanissimi. Allo studente che mi chiede “Ma insomma, cos’è un vettore?” non posso rispondere, perché vettore potrebbe essere qualsiasi cosa. Gli posso solo ripetere che cos’è uno spazio vettoriale, invece: come si devono comportare due certe operazioni, su oggetti la cui natura è inessenziale. In fondo è questa la profonda ragione per cui dentro a un calcolatore si può simulare un’incredibile quantità di situazioni reali: il suo modo totalmente astratto di lavorare permette a noi di renderlo molte volte concreto.